The aerodynamic theory of the lifting line was first solved by Multhopp1. This
solution uses a spanwise distribution of the control points accordingly a sinus-function and is applicable to unswept wings. For the bell-shaped lift distribution ![]() a direct solution of the lifting line formula can be derived and is described here.
a direct solution of the lifting line formula can be derived and is described here.
The integral for total lift ![]() can be written as (Truckenbrodt2):
can be written as (Truckenbrodt2):
|
|
|
|
(Tru. 5.42) |
For a symetrical lift distribution this formula can be transformed:
|
|
|
|
(Equ. 00-01) |
If the spanwise control points are aranged along a "central-angle"
|
|
local lift load |
|
(Mul. 07) |
This leads to the final integration and its solution:
|
|
|
|
(Equ. 00-02) |
|
|
|
|
(Equ. 00-03) |
The total required geometrical twist
|
|
|
|
(Tru 7.64) |
The local effective angle of attack can be found with the term:
|
|
|
|
(Tru. 7.11 & 7.28) |
This term is now used in Equation (Equ. 00-01 b):
|
|
|
|
(Equ. 00-04) |
The solution for the induced angle of attack is more complex. Truckenbrodt gives the induced angle of attack
|
|
|
|
(Tru. 7.67 & 7.70) |
Using the following terms, we can transform this integrartion in the formulation as given in Multhopp:
|
|
|
|
(Equ. 00-05) |
|
|
|
|
(Mul. 13) |
This formula now has to be solved for the bell shaped lift distribution:
|
|
|
|
(Equ. 00-06) |
|
|
|
|
(Equ. 00-07) |
For this the term is split up in several parts, which can be integrated seperately. The calculation is described in the Appendix A1 . The final solution is:
|
|
|
|
(Equ. 00-08) |
This gives the required calculation method for the geometrical twist ![]() , which can be transformed, using equation (Equ. 00-03):
, which can be transformed, using equation (Equ. 00-03):
|
|
|
|
(Equ. 00-09a) |
|
|
|
|
(Equ. 00-09b) |
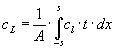
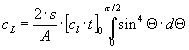 with
with 


