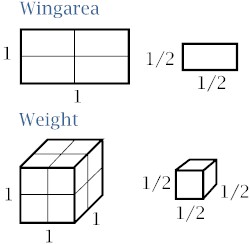
It would be super to use  data on airfoils as well. But since this area is enormous in choice, I thought we will succeed in this. But we can try to generate a data-insert-program so you can insert several (read: as much as possible) points of a drag-polar (or any other polar) you found. This way you are able to use some programs you can find on the net to generate this curve.

If somebody kwons how to work with JAVA, here is another thing that was on our minds. A page with "Pop and drag"-points to draw a half-wing. This program should help calculating the wingarea, sweepangle (1/4 chord and at the nose), AC (aerodynamic center) and CG (center of gravity) of a wing and so. It should also help drawing elliptical wings. If you are such a JAVA-wiz or -kid, contact us and we will give you more info about this program (what formulas to use, what possibilities and buttons it should have.

More theory

Changing the size

Everybody dreams of having a replica of some famous aeroplane. Mustang, Corsair, Fw-190, Mosquito would be just a few on the most wanted list. But I need to warn those who want to make a scaled version. Imagine you would like to make a 1/2 scale version of a Corsair. The wingarea and the weight will  be less than the original, of course. But the wingarea will be 1/4 of the original (1/2 . 1/2= 1/4), while the weight will be 1/8 of the original (1/2 . 1/2 . 1/2= 1/8).

Here you can see that wingarea uses two dimensions and weight uses three dimensions. That's why the relation wingarea/weight changes when scaling a airplane.

What are the consequences of these changes in the relation wingarea/weight? Well, we need to look at two different situations. First we look at scales larger than 1 (bigger than original). Here the weight rises quicker than the wingarea. This situation leads to larger wingloadings and all its problems (underpowered, high stallspeeds, clumpsy steering). Secondly we look at scales smaller than 1 (smaller than original). Now we need to look at two different phenomenons. The first is related to what we told you here above. The weight drops quicker than the wingarea. This leads to low wingloadings. These planes are more lively than the original. This sounds like fun. But remember that some WW II-airplanes were so lively and agile that they became deadly. Imagine a scales down version of such a airplane in the hands of a beginning pilot. Aaaaaah! Secondly you need to know that scaling a airplane doesn't scale the surrounding air. When using slow wings you need to keep this phenomenon in mind. What happens? A airfoil, which performs very good in a WW II-airplane, can perform less if you scale the airfoil to a handthrow model. What happens around the airfoil? The air around the airfoil seperates quicker. You can avoid this situation by choosing a airfoil that is less thick. The Reynolds-numberrange of a airfoil can help you in your choice of airfoil.

Re =	. v . k	(formula 40)
		Re = Reynoldsnumber = density medium v = velocity k = chord = viscosity medium

This can be simplified to:

Using the smallest chord and the slowest speed you will get the lowest Reynolds number the airfoil has to have. There are many lists on the net where you can find airfoils and their Reynolds number range. Be sure not to forget to check the airfoil when starting a new design. If you use a improper airfoil, you may get stalls earlier than expected and this mistake can be deadly to your model (and/or the pilot).

Also keep in mind that the performance of a airfoil depends of the used Reynoldsnumber. A certain airfoil has a higher maximum C_l when used with larger chords. Remember: larger chords leads to larger Reynoldsnumbers. When using a smaller airfoil (like RC (=Radio Controlled) -models) the Reynolds- numbers are much lower than when using the airfoil for a full-scale, piloted airplane. So don't use data (like maximum Cl, minimum drag) of  a airfoil when they are generated at lower or higher Reynoldsnumbers. A deadly mistake!

Changing (or choosing) the airfoil

This choice can be difficult, because the choice is enormous. You need to keep several thing in mind while choosing a airfoil. First, the Reynoldsnumber. Make sure your situation is located in the Reynolds number range of the airfoil. Secondly, the lift/drag relation. Every airfoil has his typical curve. We will help you in understanding these curves.

The polar

A example of a polar

Several, easy to be found points on the curve can be of great importance to you. Point 1 (C_{l max}) is easy to find. That's the point on the top of the curve. At this point you can calculate the stallspeed. Put C_{l max} into a variant of formula 1 in formula 2 (see The forces) and you get:

v stall =		W		1/2	(formula 43)
		0,5 . . Cl max . S

Point 2 shows the stall of the airfoil. Do not make the mistake by using this point to calculate the stall speed. You really need to use C_{l max} for that issue. Point 3 is the point with the lowest C_d value. That's the point on the left on the curve. At this point you get the highest speed. Point 4 is the point where the curve crosses the X-axis. Here is the point for a dive. Every point below the X-axis is related to inverted flight.
There are some other interesting points. But these need to be calculated or constructed. Point 5 needs to be constructed. To understand the importance of this point you need to know that in every point of the curve you can determine the glide angle. How? Well, just construct a line from the 0,0 point (crossing of X and Y-axis) to the point. The angle between this line and the Y-axis is the gliding angle. Point 5 is the place where the angle is the smallest. Also is the relation C_l/C_d maximal in this point. C_l/C_d is the glide ratio of the wing. The lower the glide ratio, the lower the needed power to get horizontal, powered flight. So here you can also find the point of best cruising. Remember what I said in the first part of the theory! Don't forget the dragcoefficient of the fuselage and all the rest when calculating the exact theoretical glide ratio. You need to use point 5 and increase that C_d with the other C_d's (don,t forget induced drag, later more on this item). You could use the obtained glide angle to calculate the length of the landinggear.
Point 6 needs to be calculated. This point is known as the climb ratio. Point 6 is the point where C_l³/C_d² reaches its maximum. How can you find this point quickly? Just make a spreadsheet (Excell or any similar program), fill in some points of the polar (the more, the better) and let it generate a curve (C_l³/C_d² on X-axis and C_l on Y-axis). The point on the most right is the maximum we seek.

Theoritical glide ratio

You could already read that finding the glide ratio could be easy to find. It is simply the smallest angle possible between the Y-axis and the line constructed between the origin (point 0,0) and a point on the polar curve. But a simple polar does not contain all the factors of a airplane. You still have to keep in mind the parasite drag of other components (fuselage, wheels, tail) and the induced drag.

You can now calculate the C_d increase, due to the induced drag, for every point of the polar. If you already created that spreadsheet I mentioned, it will not be hard to include this formula into the spreadsheet.

For the additional parasite drag, due to the other airplanecomponents, you need to correct the C_d values you can find in the list placed in "The forces". These values are related to the frontal area, the formula for drag (formula 12) is related to the wingarea.

You can use this correction on any airplane part.

C_D (the total airplane drag coefficient) is the result of the C_d of the wing (polar), C_di (induced drag) and the sum of all the corrected drag coefficient
(formula 46)

When you construct the curve off the total airplane drag, you can search for the theoritical glide ratio by constructing a line from the origin (point 0,0) that touches the curve. The glide angle is at this point is the smallest. The C_l/C_D ratio at this point is the theoritical glide ratio of the complete airplane.

Another angle, the effective angle of attack of the complete airplane can also be calculated. But do not mistake this angle with the geometric angle of attack (= true angle between horizontal and airfoil).

Look out about the interpretation of this formula. I don't say that the angle of attack gets less when the induced drag is larger. I say that the angle used effectively by the wing (used to create lift) gets less when induced drag gets larger. So you need more geometric angle to create the same lift.

Choosing your wingarea

Still working on this one.

Changing the wing form

As you could see in the first part, there are a few factors that you can change once you decided what wingarea you want to use. Aspect ratio and taper (multi or single taper). The choice of aspect ratio has many consequences. OK, you can choose ultrahigh or ultralow or a "normal" medium. Each has his pro and cons.
Ultrahigh will lead to very short chords. This long, slim wing leads to heavy spars. Also remember what I said about Reynolds. The smaller the airfoil, the more problems about airseparation at low speeds. But the higher the aspect ratio the smaller the induced drag and that is a good point. The smaller the induced drag the smaller the induced angle of attack (see above). So the shorter the needed landinggear.
The lower a aspect ratio the compacter the airplane and the larger the airfoil. Using this large wing you could use a lighter spar (higher spar are stronger and can be made lighter to have the same strenght). Cockpit could be integrated into the wing, which will produce less parasite drag. But low aspect ratio has a high induced drag. High induced drag means higher induced angle of attack. This means a longer landinggear. Low aspect ratios can fly under a greater angle than the high aspect ratios, so they can use their wing as a airbrake. Due to this there is no need for high-lift devices on a low aspect ratio, so the construction is made easier. They can fly slower, but there is many power needed to keep them in the air under this condition.